I don't intend for this review to get overly technical, nor should it be considered a formal analysis. As the devil's advocate, I am only putting Bill Munn's 15mm lens theory to the test. This review is only my opinion based on the information available to me. Regardless of any discrepancies in our conclusions, Bill's report was an invaluable resource and the first photogrammetric analysis of the PGF.

I'm a geomaticist by profession, with emphasis in photogrammetry. I usually work with digital images of aerial photographs which get "rectified" (flattened out) so that their content can be geo-located and mapped. The principles of photogrammetry are the same for 16mm film. Analysis of the PGF is called "close range" photogrammetry. The PGF is a sequence of still images which contain vastly more information than a group of unrelated photos. Movie film represents a time series of events allowing us to track a moving object through a scene and average all the estimates. The changing size of a figure over a sequence of frames is directly related to the distances from the camera. The farther away from the camera, the smaller the image and vice versa. This relationship allows us to measure the images and determine relative distances between frames of film. The changing camera positions also change the point of view (POV), which allow us to "triangulate" the position of objects within the site. We can then build a site model, which can be used to test the "historical" measurements of the film site.

Bill used photogrammetric software to triangulate his model of the PGF site. However, he was unable to make his model fit for a 25mm lens (25mm focal length). According to the historical data, Patty was 102' from the camera in frame 352. Bill then photographed a 6' 3" person with a 25mm lens at 102' from the camera and superimposed his image in a digital copy of frame 352 from the PGF. This comparison suggested that Patty's image was either underscaled, or her standing height was less than 5 feet. Either way, something wasn't right. Then he discovered that the Kodak K-100 16mm movie camera also came with a 15mm lens. If a wider-angle lens was used, then that might explain why Patty was underscaled. When he tried a 15mm focal length lens to create his software model it appeared to be a perfect fit. Since a 25mm focal length didn't work and 15mm seemed to fit perfectly, Bill was compelled to accept that a 15mm lens was used to shoot the PGF and his 15mm lens theory was born.

So how does a 15mm lens view look compared to a 25mm view?

One frame has been scaled up to simulate the difference between a 15mm and 25mm lens. The differences are evident. This is why Bill believes Patty was 7' 4". Her image needs to be "blown-up" to match a 25mm lens, which scales her image up 60%.

John Green went to the site of the PGF within the year and used a 16mm camera to shoot some footage of Jim McClarin walking along Patty's trackway. It isn't known how closely McClarin followed the trackway, but his image has been used to estimate Patty's height. However, there are 3 issues that make any comparisons problematic, namely: 1) how closely did he follow the trackway? 2) how close was Green's position compared to Roger's? 3) what was the lens used?

The classic comparison of McClarin and Patty is at approx. frame 352 of the PGF. This is the graphic often cited:

Patty's image towers over McClarin, who allegedly followed Patty's exact trackway. But how similar was Green's camera to the K-100 that Roger Patterson used? The McClarin footage has caused some controversy when comparing Patty to 6' 5" Jim McClarin walking along her trackway at the film site. It was very fortunate that Green shot this footage as it is the only other known film of the PGF site. Green was also very close to Roger Patterson's position during filming. However, between Green and McClarin's positions, there is the potential for a relatively large margin of error. Some of the error can be resolved by "registering" (matching up the backgrounds) in both photos. Then the differences in the foreground reflect the relative difference in camera positions. Determining whether Patty was further away from the camera than McClarin, however, is more complicated.

Bill also deduced that Roger Patterson's camera position was approximately 10 feet closer to Patty than Green. There are some obvious differences in the foreground objects, which support this. Roger was a bit closer to the log than Green, in which case Patty's image needs to be reduced according to this difference. At 100 feet from the camera, a difference of 10 feet amounts to a 10% difference in image size. This comparison would only be valid if Patty and McClarin followed the exact same path. After registering a frame from each film, I reduced Patty's image size by 10%, as seen below. But we still don't know if this is a valid comparison.

After examining a full frame from the McClarin footage, it is apparent that the field of view (FOV) of the camera lens used by Green was very close to the PGF camera lens. The size and distances between trees are very close and Green definitely used a 16mm camera (confirmed by the film back). I also suspect that he used a 25mm lens. I think the key here is to ascertain what model camera and lens type Green used. This could identify the lens used for the PGF, but not necessarily the exact focal length. How likely is it that Green's camera matched the FOV of the PGF with a 15mm lens? The standard lens for a Kodak K-100 film camera is 25mm. Find out the lens that Green used and the PGF lens issue is settled.

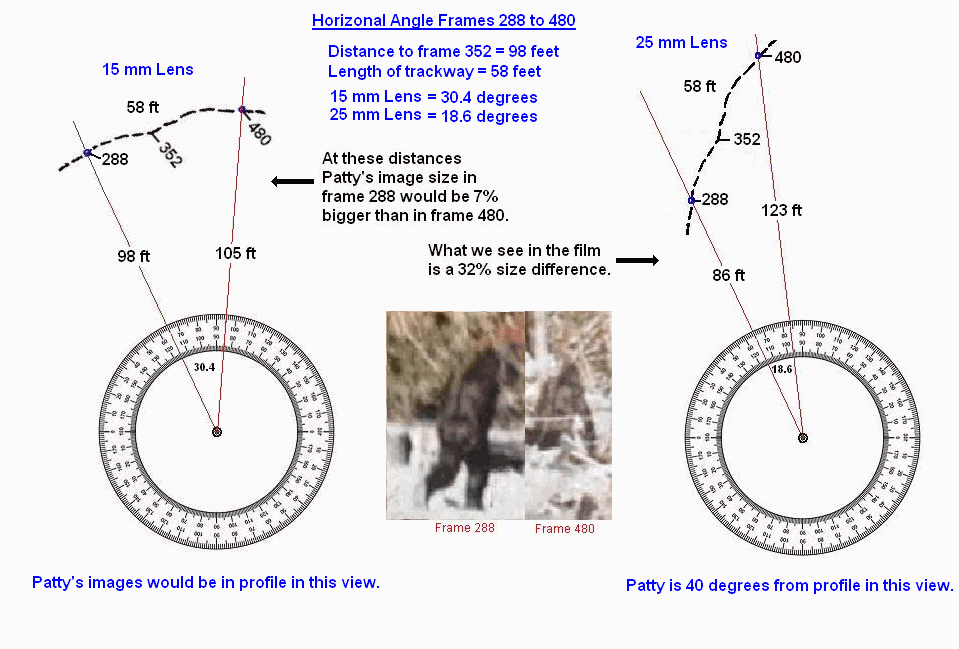
Since this information is not currently available, I decided to examine the film's FOV to see if it could reveal the lens used. I chose a sequence of frames from the PGF (288 to 480), which are within the same FOV as frame 352. This sequence of frames represents exactly 17 steps along the trackway. This part of the trackway is not a straight line, however, we can test whether the distance traversed for 17 steps was possible with a 15mm lens. A 15mm lens "widens" the angle between frames, 288 and 480, which makes the trackway distance longer. But by how much? And can we match the angle of the trackway to Patty's body orientation relative to the camera position? For example, here is the triangle that is formed by the camera to frames 288 and 480 and the trackway based on the Titmus/Krantz site map.

The FOV angle in this case is approximately 18.5 degrees. The FOV angle for a 25mm lens is actually 18.65 degrees. Coincidence?

90% of photogrammetry is solving triangles. If we can solve for this triangle, we can determine the focal length of the lens by measuring the FOV angles. Here is how the vertical FOV is determined (substitute the frame width for the frame height to get the horizontal FOV):

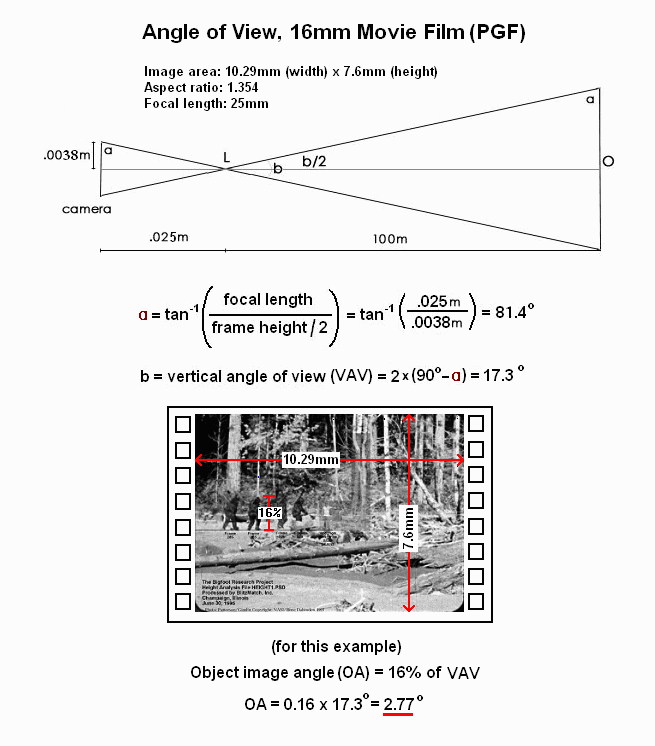
Substituting the frame width the horizontal angle of view (HAV) is:

HAV = 2 * (90 - Arctan(.025 / .005145)) = 23.26 degrees

So a full frame of the PGF has a 23.26 degrees Horizontal FOV.

 

The following graphic shows a full frame digital image of frame 352 with Patty's image in frames 288 and 480 registered to the background (60% actual size for this review). We can measure the FOV between these frames very accurately for either lens. We know the horizontal FOV for a full frame is 23.26 degrees (25mm) and 37.86 degrees (15mm).

The actual trackway from frames 288 to 480 will only fit 1 FOV and it is either 18.65 degrees (25mm) or 30.43 degrees (15mm). It is also possible that the "effective" focal length of the lens is not "on spec". The focal length of a lens can be off spec by as much as + or - 10%. The PGF lens could have been 15mm +/- 1.5mm or 25mm +/- 2.5mm. This variance makes a direct comparison problematic. We need to calibrate the focal lengths to be able to compare Patty's relative size this way. But with enough control data (relative markers), software can triangulate the effective focal length of the lens. This is the path that Bill took.

The model developed from the control data will either support or refute the historical data. Bill's model fits quite well with the historical data, however, the historical data is incomplete. There were no "cross field" measurements taken at the film site. All the distances measured were from the camera. If someone had measured the distances between some of the background trees, then the focal length could be confirmed. This is where Bill's model might break down. A 15mm lens spreads out the distances in the background by 60% so that it would be apparent which lens was used with 1 good cross field measurement.

Since no historical data is available, the next best bet it to use Patty as a walking ruler to approximate a cross-field measurement. We know the exact frames representing 2 sides of the triangle (to the camera). Let Patty's trackway represent the 3rd "irregular" side. If Patty's step length was 41" in 17 steps she would have traveled 58'. Because she didn't travel in a straight line, the length of the 3rd side of the triangle is probably closer to 56'. Keep in mind we only need to establish a maximum distance for 17 steps of the trackway. For example, if a 60" step length is required to support a 15mm lens, then you have to reject the 41" estimate and accept that Patty was a giant.

The requirements to solve the triangle are:

• the angle of the trackway

• the length of the trackway

• the distance from frame 352

• the FOV angle for frames 288 to 480

• the size change in Patty's images

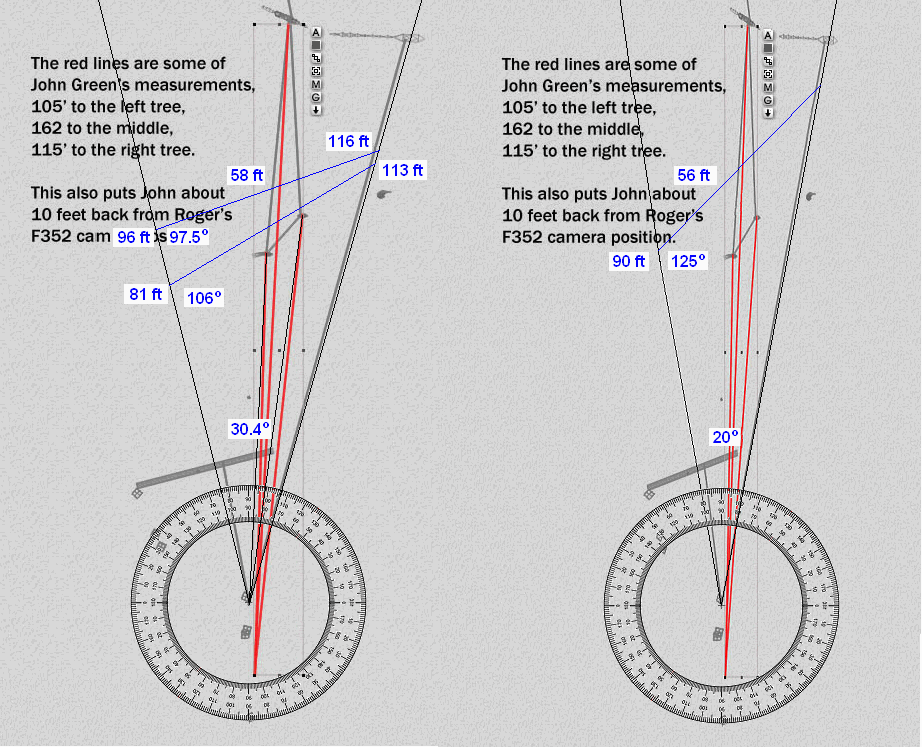
The sun cast shadows 7.5 degrees E of N during the filming (1:30PM DST Oct 20, 1967). Patty was travelling NNE. The trackway orientation relative to her profile was approx 40 to 50 degrees from frames 288 to 480. A person (or mannequin) can be angled to confirm this. If 17 steps were 58 feet, then at 100 feet from the camera a 15 mm lens would require Patty to be almost in profile, which was not the case (except near the turn).

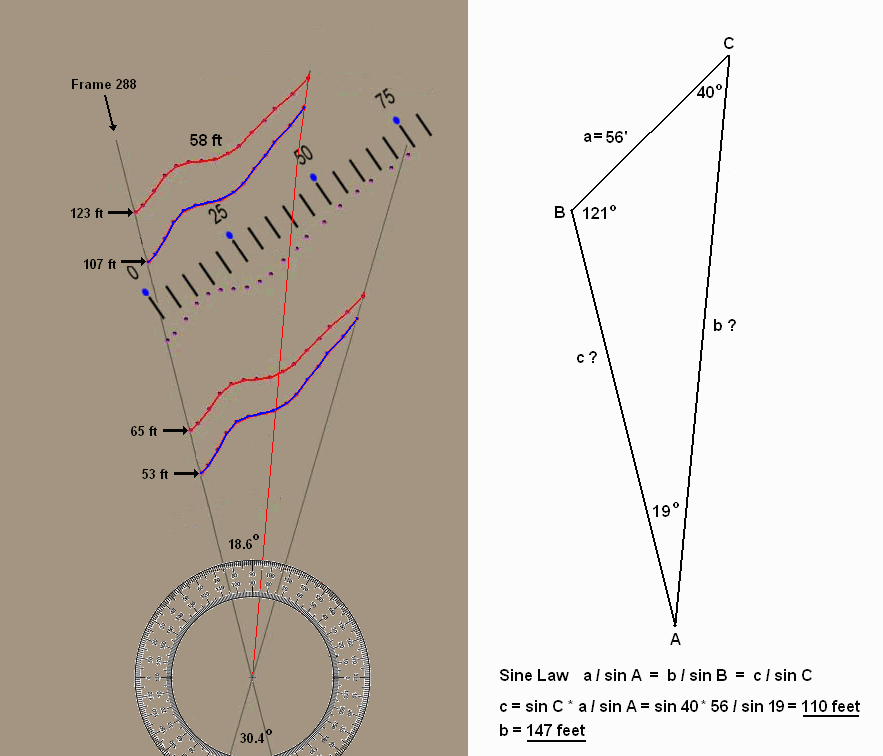
Granted, the map of the trackway produced by Titmus and Krantz has some big question marks, but the distances appear to be accurately scaled and oriented. Let's test it. According to the map and using the number of frames per step (as seen in the film 11.3 frames/step) it turns out Patty's step length was a very consistent 41-42 inches long. This jives. So when I took the overhead section of the trackway and Roger P's position for frames 288 to 480, I formed an angle, which can be tested against the FOV angle (on frame 352 above).

The distance on the map from frames 288 to 480 is 58 feet. The distance from the camera to frame 352 is 98 feet on the map (as was Bill's estimate). The angle of the trackway is the only variable left to make Bill's 15mm model fit. To make a 15mm lens fit, the FOV angle between frames 288 to 480 must be 30.35 deg. (measured directly from a full frame). But this angle just doesn't work. Only if Patty's trackway was nearly parallel to the camera plane (which it was not) can you achieve a 30+ degree FOV angle with 1 side = 58 feet at a distance of 100 feet from the camera. The FOV differences between a 15mm and 25mm lens are large and should be evident. For a 15mm lens the image size for frame 288 would have to be the same size as frame 480, which would place them at the same distance from the camera. This was not the case.

If Patty's orientation was 41 deg from profile, and her track length was 58 feet (frames 288-480), then a FOV angle of 30.4 degrees could only be achieved if the camera was 37 feet away. By all historical estimates, this was not the case and, IMO refutes a 15mm lens. But this is just 1 example from the historical data, which is by no means conclusive.

The change in Patty's image size over 192 frames of film appears geometrically impossible with a 15mm lens at a mid-distance of 100 feet from the camera. This is independent of the Titmus/Krantz map. The trackway would need to be much more than 58 feet to achieve Patty's body angle with respect to the camera. In other words, a 15mm lens would require a much longer step length than 41". Is it possible these longer steps were overlooked? Seems unlikely there was a conspiracy to cover up these long tracks.

So what kind of triangle does Bill's model make based on a 15mm lens? The following graphic show's his triangle and Patty's trackway in purple dots. The red line represents the FOV for a 25mm lens. Note that Bill's model sets the trackway length at almost 75 feet for 17 steps. That's a 53" step length. Could everyone have missed 53" steps?

Below is a diagram of Bill's 15mm model and Rene Dahinden's historical site model (reproduction by Chris Murphy). It appears that Rene's diagram got the angles right as well as the distances. Rene's model happens to coincide with a 25mm lens to within 1%. I doubt he could have reverse engineered this. That's the 2nd historical model that contradicts a 15mm lens.

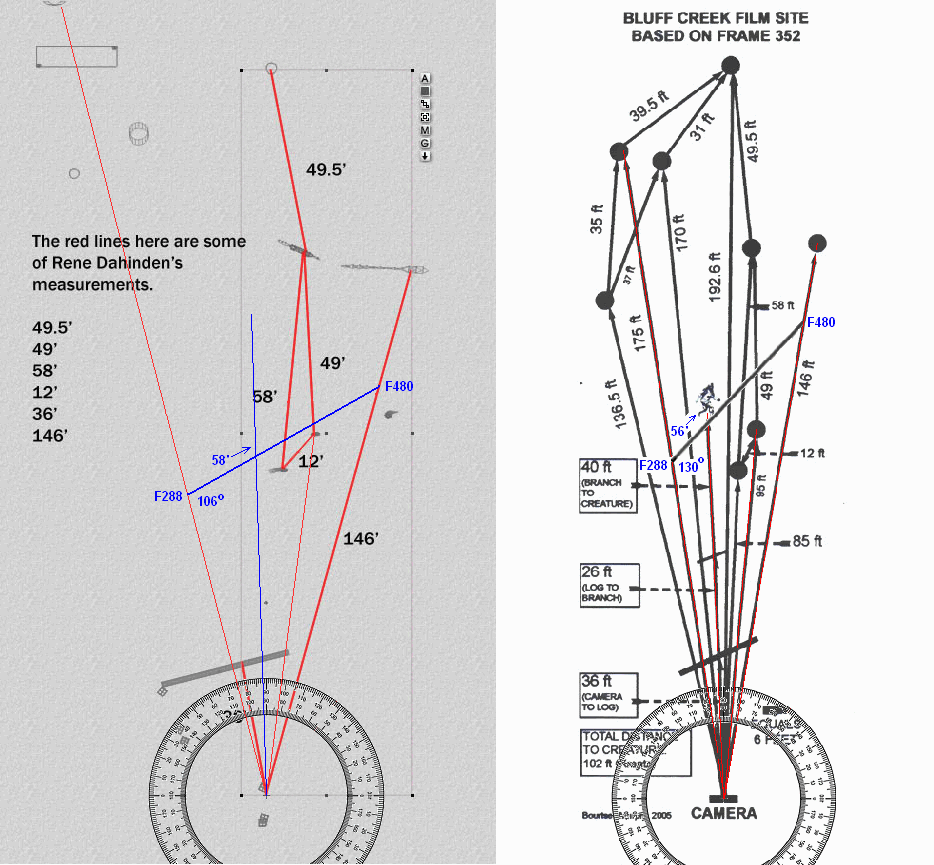
Both these models appear to fit the various objects in the scene to correct scales. All the distances from the camera are the same for both models. However, the horizontal distances between objects are different and wrong for at least 1 of the views. Very few horizontal distances were recorded, which would have readily excluded 1 of the views. One model was derived from the film and the other from surveyed measurements at the film site.

Since Patty’s body orientation is always more than 106 degrees over the trackway, (except at the turn) it is assumed that the 15mm FOV must be distorted. The FOV has been stretched exactly 60% according to the difference between a 15mm and 25mm lens.

The next diagram shows Bill's model next to a 25mm model (using Bill's site objects and frames). Both models represent a "near" solution for all distances from the camera. But only 1 model has the horizontal (cross field) distances correct. Otherwise, one view is only "nearly" correct.

Here is Rene Dahinden's original diagram of the PGF site. Once again it matches the FOV for a 25mm lens. The angle of the trackway (dashed line) is incorrect, however. Patty would have been in profile and her image would be the same in frame 288 as frame 480. Which was not the case.  It is assumed that the field measurements were correct, the trackway was not.

Calibrating The Lens

To "calibrate" a 16mm camera lens and determine the "effective" focal length requires measuring the physical image area on the film back. If a ruler is placed in the frame at a known distance from the camera you can calculate what the image height should be for a given focal length. If the theoretical image size is different from the actual image, then we know the effective focal length is not on spec. If the actual image is too large, then the focal length is > than spec, and vice versa. The measured size differences can then give us the effective focal length (offset) of the lens.

When Bill filmed a walking 6' 3" guy with a 15mm lens and superimposed it onto frame 352, he didn't calibrate the lens' effective focal length. If his 15mm lens had a 16.5mm effective focal length, then it would explain why the image of the 6' 3" guy was overscaled. This is providing his image wasn't already overscaled when his film frame was digitally scanned. But if a lens' focal length is exactly 15mm, then the image size will match the theoretical image size, otherwise, it's off spec.

Bill's estimated height for Patty in frame 352 was 15% of the frame height. But I believe Bill was referring to Patty's walking height. There is a significant variance between Patty's walking/standing heights. Patty's 41" step length, bent knees and forward posture combine to give her over a foot of height difference. At her lowest point she's barely over 5 ft tall. This is probably why there is so much controversy over her height estimates.

To get an approximation of the standing versus walking height difference, lean up sideways against a wall. Spread your legs out 41", bend your knees, stoop over and measure your height on the wall. For a 6 ft standing height, the walking height is reduced over a foot. Which is 17.4%.

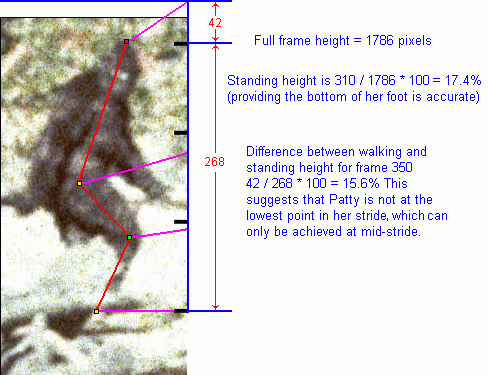
Since Patty walks compliantly ("groucho" walks), we never actually see her standing height. She keeps her head level and her height variance is relatively small. But the variance between her walking/standing height is very large. JREF member Tube experimented in beach sand and found that compliant "groucho" walking was an effective way to sustain long strides and keep your head level.

When we walk, our high point is almost our height. This doesn't appear to be the case for Patty. Standing/walking height variance for most humans is 8-10%, 18-20% for Patty. Which is atypical regardless of her height.

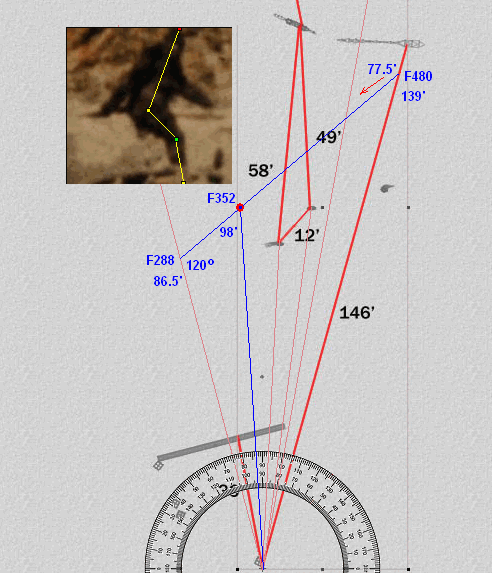
Now lets flip the coin and let Patty's step length be as long as is needed to complete Bill's 15mm triangle. What is essential, however, is that Patty's body orientation matches the images for frames 288 & 480. For this we need to create as large a trackway angle as possible, while still placing it thru frame 352 at 98 feet from the camera. IMO, we need to get the trackway angle at frame 288 to be at least 120 degrees. I don't think this is quite enough, but for argument sake let's make this the lower limit.

Here are the numbers:

Trackway
========

• Frame 288 = 120 degrees (max attainable for 15mm model)

• This puts the trackway length at 77.5' for 17 steps or a 54.7" step length

Frame 352
=========

• 98 feet from camera

• Image Height (standing) = 180 pixels / 961 pixels = 18.7% Vert FOV

• Vertical FOV (15mm) = 28.43171 degrees

• Standing Height = 98 * tan(.187*(28.43171/2))*12*2 = 109.2" or 9' 1"

Based on Bill's model, Patty's height at frame 352 = 9' 1". Patty's estimated height for frame 288 is a more modest 8' 7". Shrinking the trackway angle would shorten the trackway (& step length), but it would also put the body angles out of reach. And all this is based on a variable step length.

Estimating the Effective Focal Length

By solving the 17-step triangle, we can estimate the effective focal length. The solution represents an optimal fit of the variables. This is more in line with an error analysis, which explores the range of variables used to construct the triangle. We must ask ourselves, what angle is Patty travelling relative to the camera so that her images look like the following:

To solve this problem we need to use the following relationship:

The distance from the camera to frame 288 divided by the distance from the camera to frame 480 = the image size of Patty in frame 480 divided by the image size of Patty in frame 288. This is a direct, inverse relationship that is independent of the distances to the camera (sides of the triangle).

The following diagram illustrates how to use this scale factor to calculate the sides and angles of the triangle:

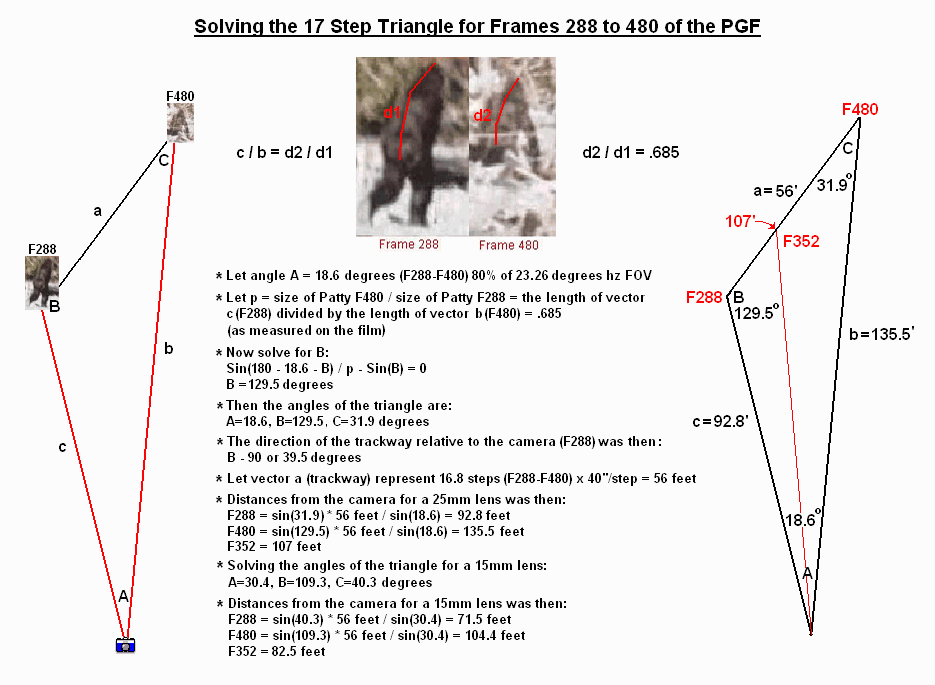
So what was Patty's standing height based on these numbers?

Her image height in frame 288 is approx. 170 pixels. The height of a full frame is 961 pixels. This is 17.7% of the full frame height. However, this represents Patty's walking height. If we "stand her up", we could add approx. 18% to her image height. Then 170 + 18% = 200 pixels. 200 / 961 = 20.8% of the frame height.

For a 25mm lens the full frame height VAV (vertical angle of view) is 17.3 degrees. Using the lens equation, Patty's height comes to 69", or 5' 9". IMO, this is likely too short an estimate. Therefore, I suspect that the trackway length was underestimated, and/or the trackway angle is not steep enough, and/or the effective focal length of the lens was less than 25mm. At any rate, if these angles are even close, then a 15mm lens doesn't create a steep enough angle for the trackway and the distances from the camera are too short.

So what angles and distances are required to bring Patty's height to 74" (6' 2") and 86" (7.2") for example? And what is the optimal focal length for a solution?

I developed a computer algorithm that tests a range of parameters required to derive these standing heights.

All combinations of variables that result in either standing height (e.g. 74" or 86") are listed for the following lenses: 22.5mm, 25mm, 27.5mm, 13.5mm, 15mm, 17.5mm. Since the manufacturer's specifications indicate a lens' effective focal length can vary by as much as 10%, I have assumed that a 25mm lens could have an effective focal length of +/- 10%, or +/- 2.5mm for a 25mm lens and +/- 1.5mm for a 15mm lens.

The following link displays the range of test values applied to the algorithm. I have edited the output to include only the best candidate triangles for each lens type.

Testing the PGF Lens for "The Munns Report"

___________________________________________________________________

Conclusions:

None of the scenarios for the 13.5, 15 & 17.5 mm lenses matched the angle of the trackway as estimated by Patty's body orientation in frames 288 & 480. This in effect eliminates the possibility that a 15mm lens +/- 10% was used to film the PGF.

The best-fit scenario was achieved with a 22.5mm lens. Here is the corresponding triangle:

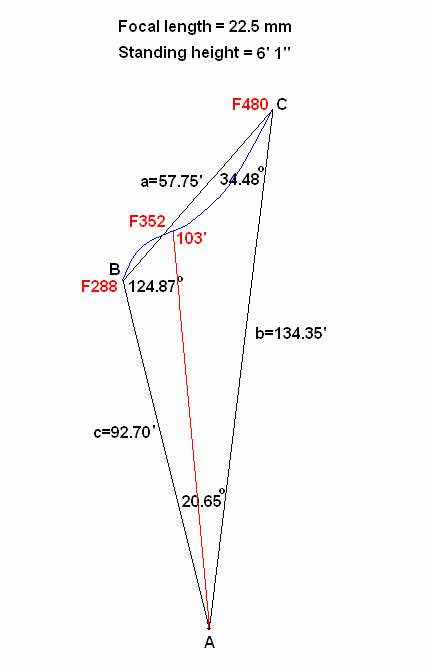
Since I believe Patty's image height (pixels) was originally underestimated, the standing height for the above scenario should be revised to 6' 3", and the optimal focal length to 23mm.

The following exercise shows image sizes for several focal lengths. There is no interpretation involved. The exact pixel heights can be calculated for each focal length for a 6' 3" figure. If the effective focal length has not been calibrated, then the theoretical image size might not match the actual image size.

The lens equation for a 75" height at 102' from the camera for a 15mm focal length is as follows:

• The vertical field of view for a 15mm lens is: 2 * (90 - arctan(.015 / .0076/2)) = 28.43171 degrees

• The full frame height in pixels = 961 (for the images above)

• Then the lens eqn is: 102ft * tan(119 / 961pix * (28.43171deg / 2)) * 12 * 2 = 75.235"

• This puts a 6' 3" image height at 119 pixels, which I scaled the figure to next to Patty.

• At this point there are no subjective measurements. What you see are the theoretical image heights if the focal length of the lens is on spec.

• Using some interpretation for the next step, however, Patty's image height is 180 pixels (18.7% full frame height).

• This puts her standing height at 9' 5", which is extreme, sasquatch or otherwise.

Here is the foot ruler used to estimate the distance from the camera for frame 72. If the foot ruler is reduced by 18%, then Patty's distance from the camera is 176 feet. This is a difference of over 30 feet. Could frame 352 have been 130 feet from the camera instead of 100 feet? None of the historical data confirms this.

The Tree Shadows

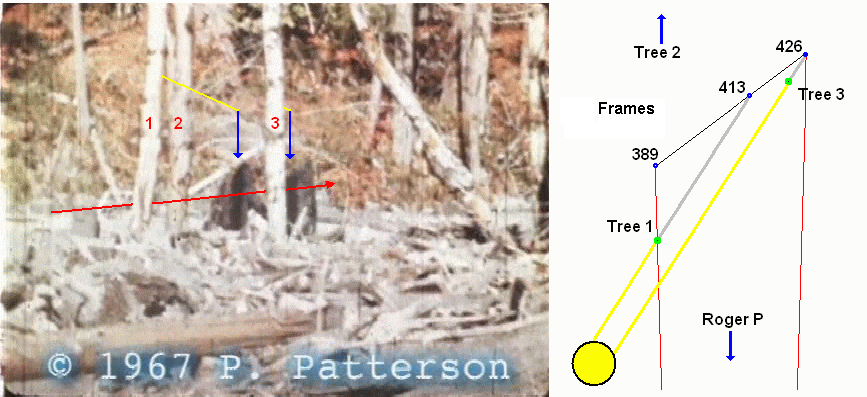
Using a full frame (352) we can estimate the angles traversed as Patty crosses these shadows. Then it is a case of solving these distances geometrically. (The following diagrams are to scale).

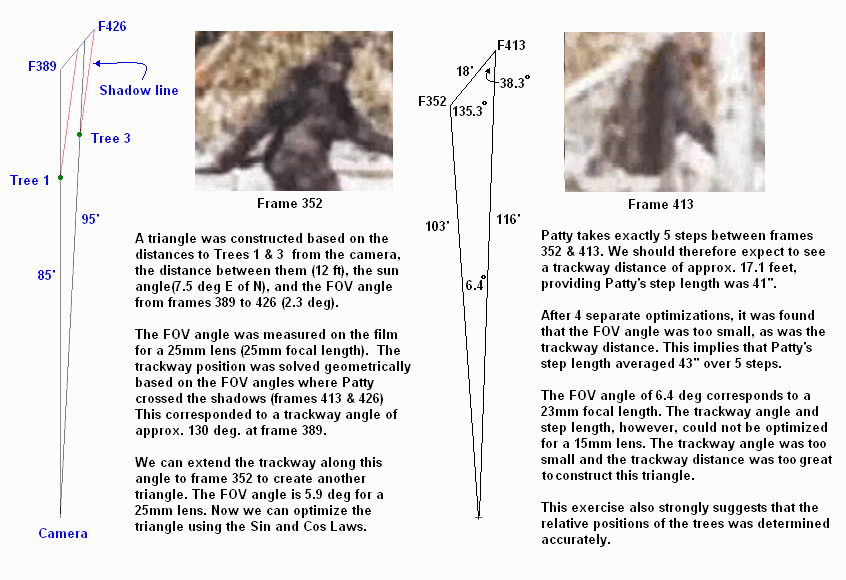
Summary

The following list summarizes the objections to the 15mm lens theory covered in this review:
 

• The foot ruler must be underscaled by over 23% to measure Patty to over 7.4' (she actually measures over 9' for a 15mm lens)

• For a 15mm lens, the trackway scales too long if Patty's step length is anywhere near 41", which is also indicated by her leg angles. The Titmas/Krantz diagram suggests a 41" step length (11.3 frames/step) over the trackway.

• The trackway angle required for a 15mm lens is too small to fit through frame 352 at 98' from the camera. This angle needs to be almost 20 degrees bigger, which was determined independent of the step length. Any steeper an angle puts the end of Patty's trackway (frame 480) past the tree marker instead of in front of it. This impossible triangle is based on the 15mm model.

• Patty's initial "standing" height was underestimated relative to a full frame to be 15% when it appears to be over 18%. Patty's walking height is over 18% shorter than her standing height (a normal human's is around 10%). It is assumed this is due to her long step length, bent knees and forward posture.

• The angles of Rene Dahinden's overhead site map match a 25mm lens. As does the Titmas/Krantz trackway map. It is doubtful they reverse engineered this, even if the maps were not exactly to scale.

• Software solutions can be wrong. Even if they seem to create a model that fits. They can converge to the "nearest" solution. Especially in this case where a 25mm focal length doesn't fit.

• The McClarin footage was shot with the same lens as the PGF, and odds are it was not with a 15mm lens.
   

There are 2 simple methods for resolving the issue of the lens used to shoot the PGF, namely:

1) Determine what lens was used to shoot the McClarin footage. It is close enough to the PGF to ascertain whether a 15mm lens was used.
2) Obtain cross-field measurements for distant objects in the PGF. This will confirm the FOV.

Otherwise, through various photogrammetric methods, the FOV can be established to within a reasonable degree of accuracy, which will positively identify the lens used.

Note that this review does not represent a formal analysis and none of my examples were conducted to photogrammetric standards. A formal study would require an error analysis to support any conclusions. This exercise was only intended to test the 15mm lens theory. However, there is strong evidence that the actual effective focal length of the lens can be resolved. My informal study suggests that a 23mm focal length optimally fits the historical data. However, I doubt that a Kodak Cine Ektar II 25mm lens was off spec by that much, which in my opinion puts the accuracy of the historical data in question. Unless these distances are confirmed, the true focal length of the lens must remain unresolved.
 

______________________________________________________________________

Many thanks to Bill Munns for providing the imagery and research data for this review.
 

Copyright © 2009 Gigantofootecus

Back